最小二乘直线拟合

简介

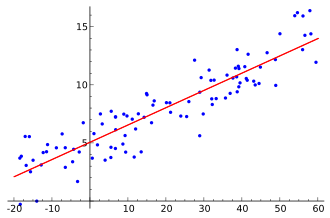
简单介绍了最小二乘法原理，以直线拟合为例结合原理出发推导了拟合算法过程，最后c++实现拟合算法。直线拟合.png

最小二乘法

最小二乘法（英文：least square method)是一种常用的数学优化方法，所谓二乘就是平方的意思。这平方一词指的是在拟合一个函数的时候，通过最小化误差的平方来确定最佳的匹配函数，所以最小二乘、最小平方指的就是拟合的误差平方达到最小。

推导过程

以直线拟合为例，已知有一组平面上的点集 $(x_1, y_1), (x_2,y_2),…(x_n,y_n)$ 。基于这些点拟合一条直线，设直线方程为 $y = ax + b$ 那么那么算法的输入就是这些点集，需要求取的为直线方程的参数a,b。

（1）平方偏差之和为 $S_{\epsilon^2} = \sum_{i = 1}^{n}{(y_i - y)}^2$ $= \sum_{i = 1}^{n}{(y_i - (ax_i + b))}^2$

那么，以上公式已知的是 $x_i, y_i$ , 未知且要求取的是a、b。不同的a、b会得到不同的 $S_{\epsilon^2}$ ，求取的是在 $S_{\epsilon^2}$ 最小的时候求取a、b。这是一个二元(a,b)函数,此问题实际上就是多元函数的极值与最值问题，要求解函数极值时二元变量数值，这里要用到二元函数取极值的必要条件

$设z = f(x,y)在点(x_0, y_0) \begin{cases} \text{一阶偏导数存在} \ \text{取极值}\end{cases}$

则

$f_x^,(x_0,y_0)=0$

以及

$f_y^,(x_0,y_0)=0$

那么对 $S_{\epsilon^2}$ 求偏导且使得偏导为0，此时 $S_{\epsilon^2}$ 取得极值点最小值

$\frac{\partial}{\partial{a}}{S_{\epsilon^2}} = \sum_{i=1}^n{2(y_i -(ax_i + b)(-x_i))=0}$

$= \sum_{i=1}^n{(ax_i^2 + bx_i - y_ix_i)=0}$ $=> (\sum_{i=1}^n{x_i^2})a + (\sum_{i=1}^n x_i)b = \sum_{i=1}^n{y_ix_i}$

$\frac{\partial}{\partial{b}}S_{\epsilon^2} = \sum_{i=1}^n2(y_i -(ax_i + b)(-1) = 0$

$= \sum_{i=1}^n(ax_i + b - y_i) = 0$

$=> (\sum_{i=1}^nx_i)a + nb = \sum_{i =1}^n y_i$

联立两式可得方程组

$\begin{cases}(\sum_{i=1}^n{x_i^2})a + (\sum_{i=1}^n x_i)b = \sum_{i=1}^n{y_ix_i} \ (\sum_{i=1}^nx_i)a + nb = \sum_{i =1}^n y_i\end{cases}$

求解方程组可得a、b的值。将方程组转为矩阵形式表示

${\begin{pmatrix} \sum_{i=1}^n{x_i^2} & \sum_{i=1}^n x_i \ \sum_{i=1}^nx_i & n \end{pmatrix}} {\begin{pmatrix} a \ b \end{pmatrix}} = \begin{pmatrix}{\sum_{i=1}^ny_ix_i} \ {\sum_{i=1}^ny_i} \end{pmatrix}$

倘若给点集的每个点加上权重，方程组则变为

$\begin{cases}(\sum_{i=1}^n{x_i^2}w_i)a + (\sum_{i=1}^n x_iw_i)b = \sum_{i=1}^n{y_ix_iw_i} \ (\sum_{i=1}^nx_iw_i)a + {\sum_{i=1}^n w_i} = \sum_{i =1}^n y_iw_i\end{cases}$

矩阵表示

${\begin{pmatrix} \sum_{i=1}^n{x_i^2w_i} & \sum_{i=1}^n x_iw_i \ \sum_{i=1}^nx_iw_i & {\sum_{i=1}^n w_i} \end{pmatrix}} {\begin{pmatrix} a \ b \end{pmatrix}} = \begin{pmatrix}{\sum_{i=1}^ny_ix_iw_i} \ {\sum_{i=1}^ny_iw_i} \end{pmatrix}$

实现代码

实现思路

（1）输入点集 $(x_1, y_1), (x_2,y_2),…(x_n,y_n)$ （2）根据点集数据和权重系数分别计算出 ${\begin{pmatrix} \sum_{i=1}^n{x_i^2w_i} & \sum_{i=1}^n x_iw_i \ \sum_{i=1}^nx_iw_i & {\sum_{i=1}^n w_i} \end{pmatrix}}$ 以及

$\begin{pmatrix}{\sum_{i=1}^ny_ix_iw_i} \ {\sum_{i=1}^ny_iw_i} \end{pmatrix}$

矩阵。（3）使用OpenCV解矩阵函数cv::solve()计算出

${\begin{pmatrix} a \ b \end{pmatrix}}$

下面放出函数实现，完整代码已托管在github,如果觉得有对你有所帮助，不妨给个star吧。代码链接：https://github.com/mangosroom/machine-vision-algorithms-library/tree/master/src/linefit

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


void mv::LineFit::FitLineByRegression()
{
    // 设置权重 | weights setting
    _weigths = std::vector<double>(_points.size(), 1);

    // AX = B
    // 构造A矩阵 | Construct A mat
    const int N = 2;
    cv::Mat A = cv::Mat::zeros(N, N, CV_64FC1);

    for (int row = 0;row < A.rows;row++)
    {
        for (int col = 0; col < A.cols;col++)
        {
            for (int k = 0;k < _points.size();k++)
            {
                A.at<double>(row, col) = A.at<double>(row, col) + pow(_points[k].x, row + col) * _weigths[k];
            }
        }
    }

    //构造B矩阵 | Construct B mat
    cv::Mat B = cv::Mat::zeros(N, 1, CV_64FC1);
    for (int row = 0;row < B.rows;row++)
    {

        for (int k = 0;k < _points.size();k++)
        {
            B.at<double>(row, 0) = B.at<double>(row, 0) + pow(_points[k].x, row)*_points[k].y * _weigths[k];
        }
    }

    // 求解A*X = B | Solve the A*X = B
    cv::Mat X;
    cv::solve(A, B, X,cv::DECOMP_LU);

    // y = b + ax
    _result.b = X.at<double>(0,0);
    _result.a = X.at<double>(1, 0);

}//FitLineByRegression

Reference

【1】opencv学习——最小二乘法拟合直线-csdn

【2】最小二乘法本质是什么-知乎

本文由芒果浩明发布，转载请注明出处。本文链接：https://blog.mangoeffect.net/opencv/least-square-method-line-fit.html

微信公众号