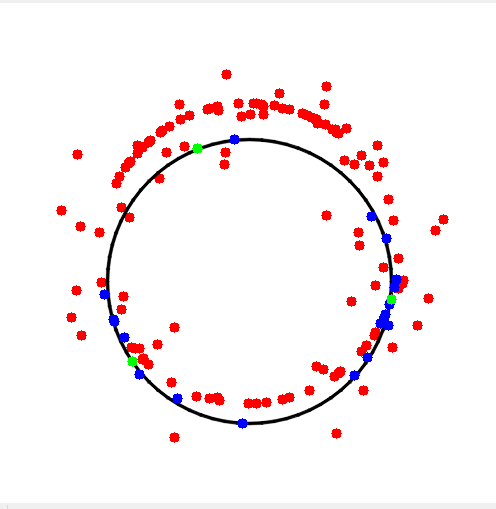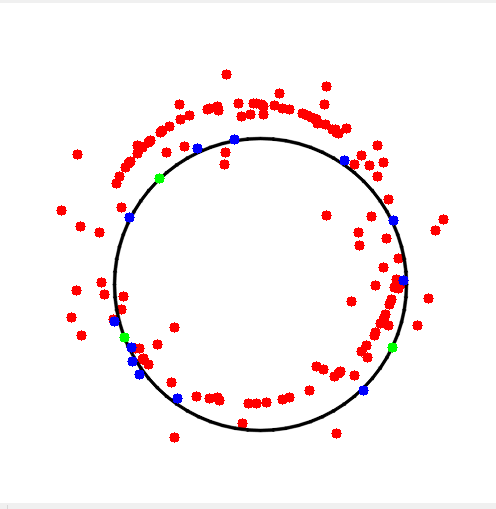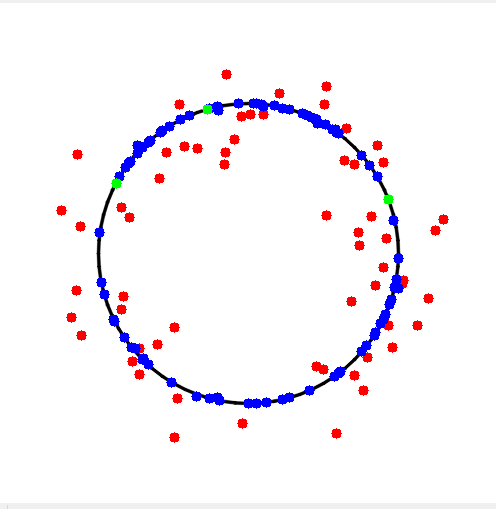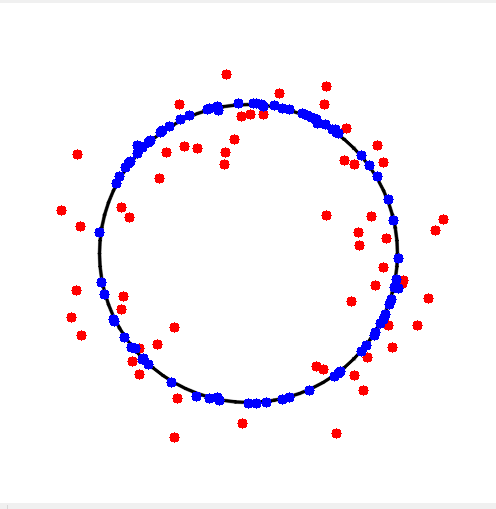
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
|
#include "opencv2/opencv.hpp"
#include <iostream>
#include <vector>
#include <random>
#include <numbers>
std::tuple<int, int, int> GetSample(const int& index_size,
const std::vector<std::tuple<int, int, int>>& sampled_indexes)
{
assert(index_size > 2);
static std::random_device rd;
static std::mt19937_64 gen(rd());
static std::uniform_int_distribution<int> dist(0, index_size - 1);
while (true)
{
std::vector<int> index = { dist(gen),dist(gen),dist(gen) };
if (index[0] == index[1] || index[0] == index[2] || index[1] == index[2]) { continue; }
std::sort(index.begin(), index.end());
bool has_sampled = false;
for (auto& [i, j, k] : sampled_indexes)
{
if (index[0] == i && j == index[1] && k == index[2])
{
has_sampled = true;
break;
}
}
if (has_sampled) { continue; }
else { return { index[0], index[1], index[2]}; }
}
}
void Show(const std::vector<cv::Point2f>& all_pts,
const std::vector<cv::Point2f>& inlier_pts,
const std::vector<cv::Point2f>& sample_pts,
const int windows_size,
const cv::Point2f& center,
const float radius)
{
cv::Mat image = cv::Mat(windows_size, windows_size, CV_8UC3, cv::Scalar::all(255));
for (auto& p : all_pts)
{
if (p.x >= 0 && p.x < windows_size && p.y >= 0 && p.y < windows_size)
{
cv::circle(image, p, 5, { 0, 0, 255 }, -1);
}
}
cv::Point2f p1, p2;
cv::circle(image, center, radius, { 0, 0, 0 }, 2, cv::LINE_AA);
for (auto& p : inlier_pts)
{
if (p.x >= 0 && p.x < windows_size && p.y >= 0 && p.y < windows_size)
{
cv::circle(image, p, 5, { 255, 0, 0 },-1);
}
}
for (auto& p : sample_pts)
{
if (p.x >= 0 && p.x < windows_size && p.y >= 0 && p.y < windows_size)
{
cv::circle(image, p, 5, { 0, 255, 0 }, -1);
}
}
cv::imshow("ransac-line-fit", image);
cv::waitKey(500);
}
void CircleFit(const std::vector<cv::Point2f>& points, cv::Point2f& circleCenter, float& radius)
{
//检查输入参数 | Check input parameters
assert(!points.empty() && points.size());
//构造矩阵 | Construct mat
double XiSum = 0;
double Xi2Sum = 0;
double Xi3Sum = 0;
double YiSum = 0;
double Yi2Sum = 0;
double Yi3Sum = 0;
double XiYiSum = 0;
double Xi2YiSum = 0;
double XiYi2Sum = 0;
double WiSum = 0;
for (size_t i = 0; i < points.size(); i++)
{
XiSum += points.at(i).x;
Xi2Sum += points.at(i).x * points.at(i).x;
Xi3Sum += points.at(i).x * points.at(i).x * points.at(i).x;
YiSum += points.at(i).y ;
Yi2Sum += points.at(i).y * points.at(i).y ;
Yi3Sum += points.at(i).y * points.at(i).y * points.at(i).y;
XiYiSum += points.at(i).x * points.at(i).y ;
Xi2YiSum += points.at(i).x * points.at(i).x * points.at(i).y;
XiYi2Sum += points.at(i).x * points.at(i).y * points.at(i).y;
WiSum += 1;
}
const int N = 3;
cv::Mat A = cv::Mat::zeros(N, N, CV_64FC1);
cv::Mat B = cv::Mat::zeros(N, 1, CV_64FC1);
A.at<double>(0, 0) = Xi2Sum;
A.at<double>(0, 1) = XiYiSum;
A.at<double>(0, 2) = XiSum;
A.at<double>(1, 0) = XiYiSum;
A.at<double>(1, 1) = Yi2Sum;
A.at<double>(1, 2) = YiSum;
A.at<double>(2, 0) = XiSum;
A.at<double>(2, 1) = YiSum;
A.at<double>(2, 2) = WiSum;
B.at<double>(0, 0) = -(Xi3Sum + XiYi2Sum);
B.at<double>(1, 0) = -(Xi2YiSum + Yi3Sum);
B.at<double>(2, 0) = -(Xi2Sum + Yi2Sum);
//解矩阵 | Solve
//求解A*X = B | Solve the A*X = B
cv::Mat X;
cv::solve(A, B, X, cv::DECOMP_LU);
double a = X.at<double>(0, 0);
double b = X.at<double>(1, 0);
double c = X.at<double>(2, 0);
//计算圆心和半径 | Calculate center and radius.
circleCenter.x = -0.5 * a;
circleCenter.y = -0.5 * b;
radius = 0.5 * std::sqrt(a * a + b * b - 4 * c);
}
void RansacCirclefit(const std::vector<cv::Point2f>& pts,
const float inlier_threshold,
std::vector<int>& inlier_indexes)
{
if (pts.size() <= 3) { return; }
if (inlier_threshold < 1e-6) { return; }
//1. 参数检查,初始化
int iterate_nums = 500; //迭代次数
float sample_points_min_distance = 5.0f; //两个采样点之间最小的距离
std::vector<std::tuple<int, int, int>> sampled_indexes;//已经采样的坐标点
sampled_indexes.reserve(iterate_nums);
std::vector<int> is_inlier(pts.size(), 0);
std::vector<int> is_inlier_tmp(pts.size(), 0);
int max_inlier_num = 0;
int sample_count = 0;
//2. 循环迭代
while (sample_count < iterate_nums)
{
//3. 随机抽取两点(采样)
auto [p1, p2, p3] = GetSample(pts.size(), sampled_indexes);
if (std::abs(pts[p1].x - pts[p2].x) < sample_points_min_distance
&& std::abs(pts[p1].y - pts[p2].y) < sample_points_min_distance
&& std::abs(pts[p2].x - pts[p3].x) < sample_points_min_distance
&& std::abs(pts[p2].y - pts[p3].y) < sample_points_min_distance)
{
continue;
}
else
{
sampled_indexes.push_back({ p1, p2, p2});
}
//4. 圆拟合
float radius = 0.0f;
cv::Point2f center;
CircleFit({ pts[p1], pts[p2], pts[p3]}, center,radius);
//5. 基于拟合的圆区分内外点
int inlier_num = 0;
std::vector<cv::Point2f> inliers;
for (int i = 0; i < pts.size(); i++)
{
auto& p = pts[i];
is_inlier_tmp[i] = 0;
double p_2_center = std::sqrt(std::pow(p.x - center.x, 2) + std::pow(p.y - center.y, 2));
if (std::abs(p_2_center - radius) < inlier_threshold)
{
is_inlier_tmp[i] = 1;
inlier_num++;
inliers.push_back(pts[i]);
}
}
Show(pts, inliers, { { pts[p1], pts[p2], pts[p3]}}, 500, center, radius);
if (inlier_num > max_inlier_num)
{
max_inlier_num = inlier_num;
is_inlier = is_inlier_tmp;
}
//6. 更新迭代的最佳次数
if (inlier_num == 0)
{
iterate_nums = 500;
}
else
{
double epsilon = 1.0 - double(inlier_num) / (double)pts.size(); //野值点比例
double p = 0.99; //所有样本中存在1个好样本的概率
double s = 3.0;
iterate_nums = int(std::log(1.0 - p) / std::log(1.0 - std::pow((1.0 - epsilon), s)));
}
sample_count++;
}
//7. 基于最优的结果所对应的内点做最终拟合
std::vector<cv::Point2f> inliers;
inliers.reserve(max_inlier_num);
for (int i = 0; i < is_inlier.size(); i++)
{
if (1 == is_inlier[i])
{
inliers.push_back(pts[i]);
}
}
float radius = 0.0f;
cv::Point2f center;
CircleFit(inliers, center, radius);
Show(pts, inliers, {}, 500, center, radius);
cv::waitKey(0);
}
int main()
{
std::random_device rd;
std::mt19937_64 gen(rd());
std::uniform_int_distribution<int> dist(0, 360);
std::normal_distribution<double> distr(0, 30);
cv::Point2f center(250, 250);
std::vector<cv::Point2f> pts;
for (int i = 1; i < 150; i ++)
{
float r = 150;
if (i % 2 == 0) { r += distr(gen); }
double theta = dist(gen);
float x = center.x + r * std::cos(theta / 180.0 * std::numbers::pi);
float y = center.y + r * std::sin(theta / 180.0 * std::numbers::pi);
pts.emplace_back(x, y);
}
std::vector<int> inliers_indexes;
RansacCirclefit(pts, 5, inliers_indexes);
return 0;
}
|