【认识】相机标定是什么？

定义

首先先了解相机标定是个什么东西，在百度百科可以查到相机标定的介绍。百度百科介绍为：

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。

如何去理解相机标定？

芒果自己简单地理解为，真实的世界物理空间是三维立体的，图像是真实世界通过摄像系统映射（或者说转换）到了二维平面。这两者之间存在着对应的关系，这种关系可以通过建立几何模型来描述（但描述有误差）。而求解这个几何模型就是相机标定的过程。

或者也可以理解为，如果把拍照过程比喻成一个函数，真实世界为自变量，图像为函数的计算结果应变量。那么标定过程就是已知自变量和应变量，去拟合（逼近）这个拍照过程的函数。既然是拟合逼近，那必然是有误差的，这也印证了上文为什么说几何模型有误差，误差的大小取决于拟合方法的优劣了，也就是标定方法的优劣。

【用途】相机标定用来干什么？

从上文简单的介绍可以了解到，标定的结果是得到三维世界与二维图像的一个映射关系（或者说转换函数）。有了这映射之后，可以想象到两种情况

• 已知三维世界中某个点的位置（世界坐标，又称物理坐标），那么可以求解到这个点在二维图像的位置（图像坐标）。
• 反过来，已知图像中某个点的位置，也可以求出它在真三维世界中的位置。

基于以上两点，就有了相机标定的以下用途。

1. 三维场景重建

既然标定已经得到了图像坐标与现实世界的三维坐标之间的关系，那么标定后的相机理论上是可以用于三维重建的，只不过三维重建实现的过程要更为复杂，不仅仅是标定就可以解决了，还需要特征提取和立体匹配等过程处理。

2. 畸变矫正

用于减少畸变，通过标定求出相机的畸变参数，从而相应地调整图像以减少图像边缘的畸变。

3. 实现与机械手坐标系的统一

此用途为最广泛的标定作用了，在机器视觉行业里，大多数的相机都需要进行标定，从而获知拍摄物体的位置，从而与机械手统一坐标，让机械手可以准确的获知物体的准确位置。

【原理】如何进行相机标定？

与标定相关的一些概念

三坐标系

世界坐标系

世界坐标系（world coordinate）(Xw,Yw,Zw)，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置，世界坐标系可根据实际的情况而设定建立。

相机坐标系

相机坐标系（camera coordinate）(Xc,Yc,Zc)，也是一个三维的直角坐标系，坐标系原点位于镜头的光心，x,y轴与像平面的两边平行展开，z轴为镜头的光轴，与像平面垂直。

图像坐标系

图像坐标系（image coordinate）（Uo,Vo),为一个二维的平面直角坐标系，原点位于图像的正中心。

像素坐标系

像素坐标系（pixel coordinate）（U,V）,也是一个二维平面直角坐标系，原点位于图像的左上角处，常用于程序中访问图像像素点。

总结四个坐标系，一幅图像的采集流程看，由外到内

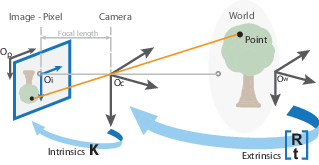
• 世界坐标系很直观地表示树在现实中的位置，坐标原点自由设置（如树根）；
• 相机坐标系则以相机光心为原点，沿着光轴方向为z轴，像面平行展开的x、y轴构成的平面。
• 图像坐标系为相机的成像界面，原点中心为顺延光轴，即图像中心。
• 像素坐标系则为我们常用程序访问图像的格式，坐标系原点为图像左上角。

外参数矩阵

外参矩阵用于转换两个三维坐标系的转换，在标定中负责转换世界坐标系到相机坐标系。

内参数矩阵

内参矩阵模拟的是针孔成像的原理，负责将三维的相机坐标转为二维的图像坐标。

畸变参数矩阵

畸变参数矩阵用来矫正畸变，内参矩阵将三维相机坐标的世界转为二维图像是理想条件下的转换，真实中是有误差的，而畸变参数就是描述这个误差，从而用于消除误差。

以上的三个参数便是相机标定要求解的参数，

标定方法

一般的标定流程，下面简单地介绍标定流程，此流程不考虑畸变。

1-世界坐标系转为相机坐标系

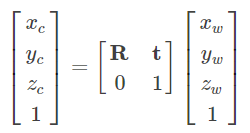
其中R为33的旋转矩阵，t为31的平移矢量，(xc,yc,zc,1)T(xc,yc,zc,1)T为相机坐标系的齐次坐标，(xw,yw,zw,1)T (xw,yw,zw,1)T为世界坐标系的齐次坐标。

2-相机坐标系转为图像坐标系

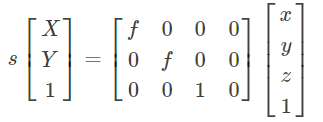
其中，s为比例因子（s不为0），f为有效焦距（光心到图像平面的距离），(x,y,z,1)T(x,y,z,1)T是空间点PP在相机坐标系oxyzoxyz中的齐次坐标，(X,Y,1)T (X,Y,1)T是像点pp在图像坐标系OXYOXY中的齐次坐标。

3-图像坐标系转为像素坐标系

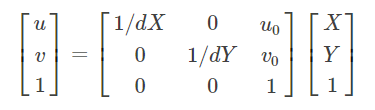
其中，dX、dY分别为像素在X、Y轴方向上的物理尺寸，u0,v0为主点（图像原点）坐标。

4-世界坐标系转换为像素坐标系

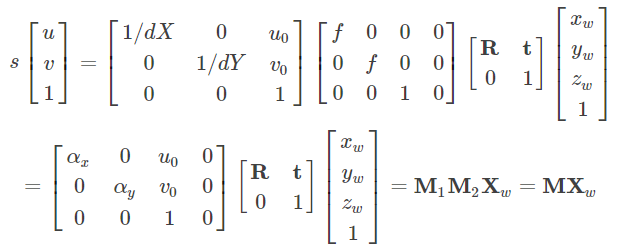
其中，αx=f/dXαx=f/dX、αy=f/dYαy=f/dY，称为uu、vv轴的尺度因子，M1M1称为相机的内部参数矩阵，M2M2称为相机的外部参数矩阵，MM称为投影矩阵。

本文由芒果浩明发布，转载请注明来源。 本文链接：https://blog.mangoeffect.net/algorithm/camera-calibration.html

https://mango-blog-1255355814.cos.ap-guangzhou.myqcloud.com//camera-calibrate-5.png