目标
阅读完本文你将了解到以下内容:
- 什么是共生矩阵?
- 共生矩阵有哪些特征?
- 共生矩阵有何用途?
- 如何计算共生矩阵?
共生矩阵简介
取图像(N×N)中任意一点 (x,y)及偏离它的另一点 (x+a,y+b),设该点对的灰度值为 (g1,g2)。令点(x,y) 在整个画面上移动,则会得到各种 (g1,g2)值,设灰度值的级数为 k,则(g1,g2) 的组合共有 k 的平方种。对于整个图像画面,统计出每一种 (g1,g2)值出现的次数,然后排列成一个方阵,再用(g1,g2) 出现的总次数将它们归一化为出现的概率P(g1,g2) ,这样的方阵称为灰度共生矩阵。
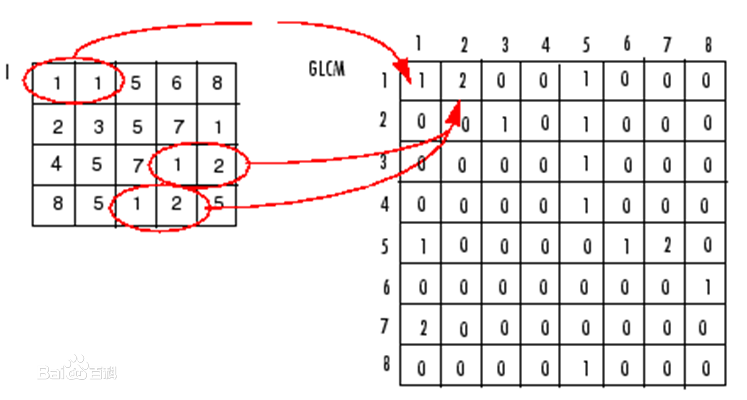
这是一种统计了图像上相隔某个距离的像素点对所具有的灰度对出现的频率情况,举个例子当a = 1, b = 1之时,灰度共生矩阵就是统计了相邻对角线(东南角)的两个像素点所对应的灰度值对的出现频率情况。因此,共生矩阵是通过研究图像中灰度的空间相关的一个描述方法。与灰度直方图一样,灰度共生矩阵描述的是图像的一个全局的信息。由于图像的纹理是由灰度的空间相关特性来描述的(纹理是由灰度分布在空间位置上反复出现而形成的),因此灰度共生矩阵用于图像的纹理特征分析。
共生矩阵的常用特征
共生矩阵常用的特征包含ASM能量、对比度、熵、自相关,假如我们另G为计算得出的灰度共生矩阵,那么这些特征可以作如下的表示。
ASM 能量
ASM能量的全称是angular second moment,即角二节矩。其数学公式描述为:
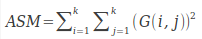
实际就是共生矩阵G每个元素的平方之和,所以也称为能量。可以通过计算发现,如果G的元素分布比较集中(即特定空间关系下像素点对的灰度值对出现概率大),那么特征ASM能量的值就比较大;如果G的元素分布比较均匀,那么得到的ASM能量的值就比较小。所以ASM反映的图像的灰度分布均匀程度以及纹理的粗细程度。
对比度
其数学公式描述为:
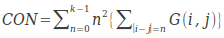 直接反映了某个像素值及其领域像素值的亮度的对比情况。如果偏离对角线的元素有较大值,即图像亮度值变化很快,则CON会有较大取值,这也符合对比度的定义。其中 。反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
直接反映了某个像素值及其领域像素值的亮度的对比情况。如果偏离对角线的元素有较大值,即图像亮度值变化很快,则CON会有较大取值,这也符合对比度的定义。其中 。反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
逆差矩
逆差矩也称反差分矩阵,其数学公式描述为:
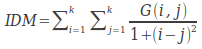 如果灰度共生矩阵对角元素有较大值,IDM就会取较大的值。因此连续灰度的图像会有较大IDM值。逆差矩反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
如果灰度共生矩阵对角元素有较大值,IDM就会取较大的值。因此连续灰度的图像会有较大IDM值。逆差矩反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
熵
其数学公式描述为:
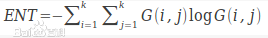
熵这一概念在很多学科都存在,含义一般用于描述的是信息的无序程度,熵越大表示信息越混乱。纹理信息也是信息的一种,而且纹理信息是图像的一个随机性的度量。所以这里的熵反映了图像中的纹理复杂程度(不均匀),熵值越大纹理越复杂。
自相关
自相关的数学公式描述为:
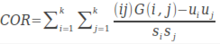
其中
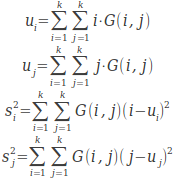
自相关反应了图像纹理的一致性。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。
最后,可以用一个向量将以上特征综合在一起。例如,当距离差分值(a,b)取四种值的时候,可以综合得到向量: h=[ASM1, CON1, IDM1, ENT1, COR1, …, ASM4, CON4, IDM4, ENT4, COR4] 综合后的向量就可以看做是对图像纹理的一种描述,可以进一步用来分类、识别、检索等。
算法步骤

|
|
|
|
reference
- 【1】百度百科-灰度共生矩阵
- 【2】图像处理、分析与机器视觉4th-74页
本文由芒果浩明发布,转载请注明来源。 本文链接:https://blog.mangoeffect.net/opencv/gray-co-occurrence-matrix.html
