1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
|
bool CircleFit::CircleFitSolve(const std::vector<cv::Point2d>& points, const std::vector<double>& weights, cv::Point2d& circleCenter, double& radius)
{
_function.params = (void *)&points;
if (radius < 0)
{
// 用最小二乘拟合的结果作为初始值
if (!LeastSquareCirleFit(points, weights, circleCenter, radius))
{
return false;
}
}
// 设置初始值
SetStartPoint(circleCenter, radius);
//经验值,初始步长设置为半径的十分之一
gsl_vector_set(_stepSize, 0, radius / 10.0);
gsl_vector_set(_stepSize, 1, radius / 10.0);
gsl_vector_set(_stepSize, 2, radius / 10.0);
gsl_multimin_fminimizer_set(_fminimizer, &_function, _startPoint, _stepSize);
int iter = 0;
int status;
do
{
iter++;
status = gsl_multimin_fminimizer_iterate(_fminimizer);
if (status == GSL_ENOPROG) // 表示无法找到更好的解了
{
break;
}
double size = gsl_multimin_fminimizer_size(_fminimizer);
status = gsl_multimin_test_size(size, 1e-2);
} while (status == GSL_CONTINUE && iter < _maxIter);
gsl_vector * out = gsl_multimin_fminimizer_x(_fminimizer);
circleCenter.x = gsl_vector_get(out, 0);
circleCenter.y = gsl_vector_get(out, 1);
radius = gsl_vector_get(out, 2);
return true;
}
double CircleFit::L1Distance(const gsl_vector * v, void * params)
{
std::vector<cv::Point2d> *vect = static_cast<std::vector<cv::Point2d>*>(params);
int N = vect->size();
double a, b, r;
a = gsl_vector_get(v, 0);
b = gsl_vector_get(v, 1);
r = gsl_vector_get(v, 2);
double sum = 0;
for (int i = 0; i < N; i++)
{
double xi = vect->at(i).x - a;
double yi = vect->at(i).y - b;
double dist = std::sqrt(xi * xi + yi * yi) - r;
sum += std::fabs(dist);
}
return sum / N;
}
void CircleFit::SetStartPoint(const cv::Point2d& center, const double& radius)
{
gsl_vector_set(_startPoint, 0, center.x);
gsl_vector_set(_startPoint, 1, center.y);
gsl_vector_set(_startPoint, 2, radius);
}
bool LeastSquareCirleFit(const std::vector<cv::Point2d>& points, const std::vector<double>& weights, cv::Point2d& circleCenter, double& radius)
{
//检查输入参数 | Check input parameters
if (points.size() < 3 || (points.size() != weights.size()))
{
return false;
}
//构造矩阵 | Construct mat
double XiSum = 0;
double Xi2Sum = 0;
double Xi3Sum = 0;
double YiSum = 0;
double Yi2Sum = 0;
double Yi3Sum = 0;
double XiYiSum = 0;
double Xi2YiSum = 0;
double XiYi2Sum = 0;
double WiSum = 0;
for (size_t i = 0; i < points.size(); i++)
{
XiSum += points.at(i).x * weights.at(i);
Xi2Sum += points.at(i).x * points.at(i).x * weights.at(i);
Xi3Sum += points.at(i).x * points.at(i).x * points.at(i).x * weights.at(i);
YiSum += points.at(i).y * weights.at(i);
Yi2Sum += points.at(i).y * points.at(i).y * weights.at(i);
Yi3Sum += points.at(i).y * points.at(i).y * points.at(i).y * weights.at(i);
XiYiSum += points.at(i).x * points.at(i).y * weights.at(i);
Xi2YiSum += points.at(i).x * points.at(i).x * points.at(i).y * weights.at(i);
XiYi2Sum += points.at(i).x * points.at(i).y * points.at(i).y * weights.at(i);
WiSum += weights.at(i);
}
const int N = 3;
cv::Mat A = cv::Mat::zeros(N, N, CV_64FC1);
cv::Mat B = cv::Mat::zeros(N, 1, CV_64FC1);
A.at<double>(0, 0) = Xi2Sum;
A.at<double>(0, 1) = XiYiSum;
A.at<double>(0, 2) = XiSum;
A.at<double>(1, 0) = XiYiSum;
A.at<double>(1, 1) = Yi2Sum;
A.at<double>(1, 2) = YiSum;
A.at<double>(2, 0) = XiSum;
A.at<double>(2, 1) = YiSum;
A.at<double>(2, 2) = WiSum;
B.at<double>(0, 0) = -(Xi3Sum + XiYi2Sum);
B.at<double>(1, 0) = -(Xi2YiSum + Yi3Sum);
B.at<double>(2, 0) = -(Xi2Sum + Yi2Sum);
//解矩阵 | Solve
//求解A*X = B | Solve the A*X = B
cv::Mat X;
cv::solve(A, B, X, cv::DECOMP_LU);
double a = X.at<double>(0, 0);
double b = X.at<double>(1, 0);
double c = X.at<double>(2, 0);
//计算圆心和半径 | Calculate center and radius.
circleCenter.x = -0.5 * a;
circleCenter.y = -0.5 * b;
radius = 0.5 * std::sqrt(a * a + b * b - 4 * c);
return true;
}
CircleFit::CircleFit()
{
_maxIter = 100; // 默认最大迭代 100 步
_function.n = 3; //变量个数
_function.f = L1Distance;
_startPoint = gsl_vector_alloc(_function.n);
_stepSize = gsl_vector_alloc(_function.n);
_fminimizer = gsl_multimin_fminimizer_alloc(gsl_multimin_fminimizer_nmsimplex, 3);
}
CircleFit::~CircleFit()
{
// 释放资源
gsl_vector_free(_startPoint);
gsl_vector_free(_stepSize);
gsl_multimin_fminimizer_free(_fminimizer);
}
|
 绘图代码
绘图代码
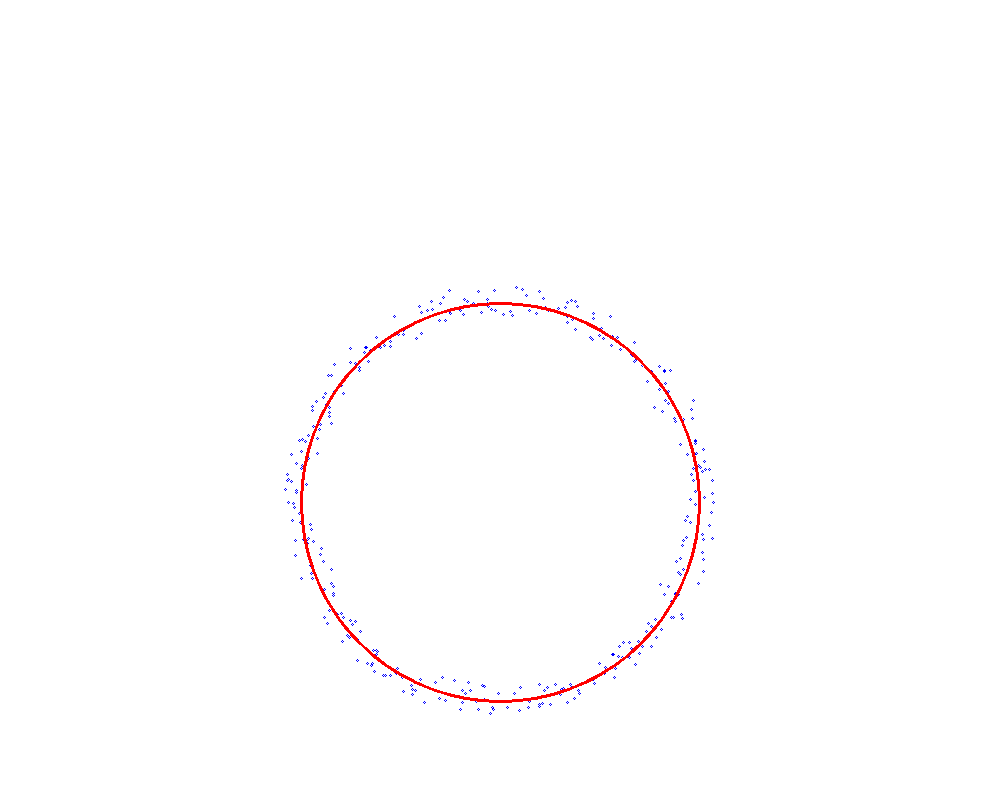
 平均绝对误差拟合效果
平均绝对误差拟合效果
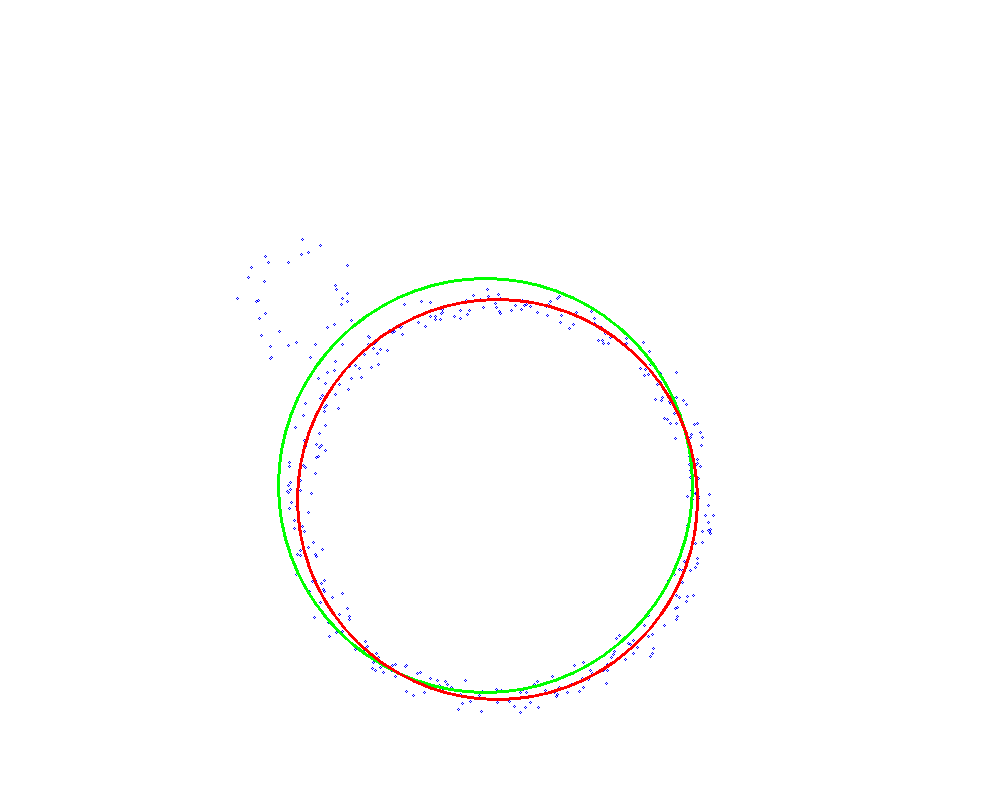
 两者对比
两者对比
 加入干扰数据
加入干扰数据
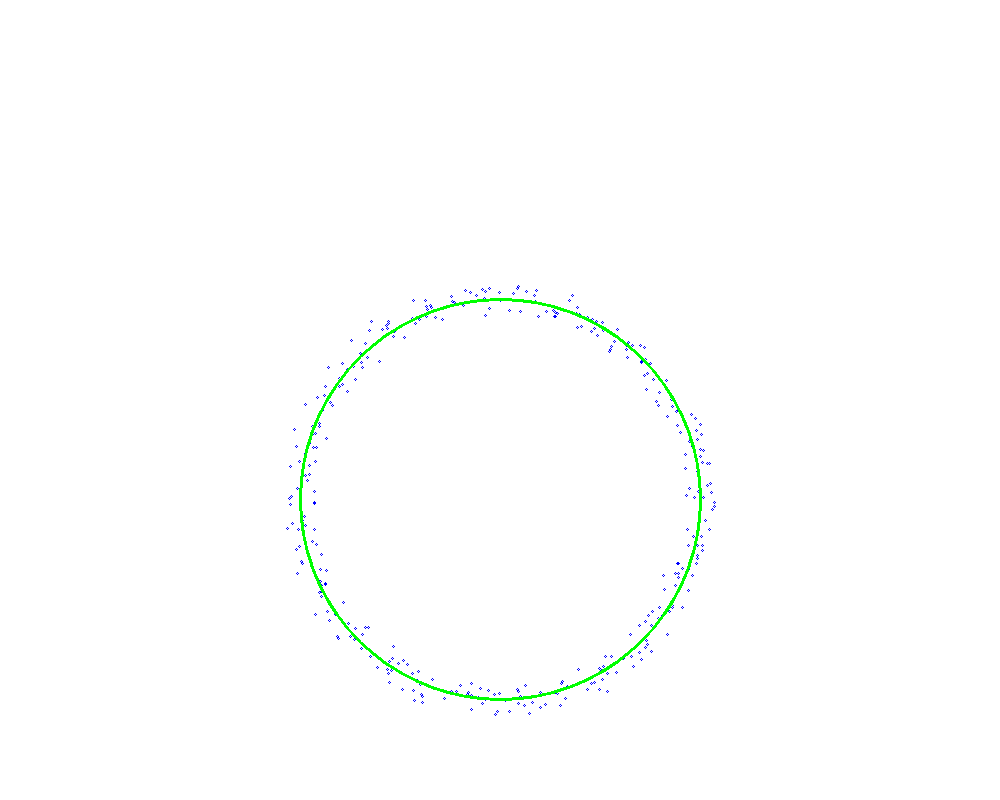
 标准最小二乘拟合效果
标准最小二乘拟合效果
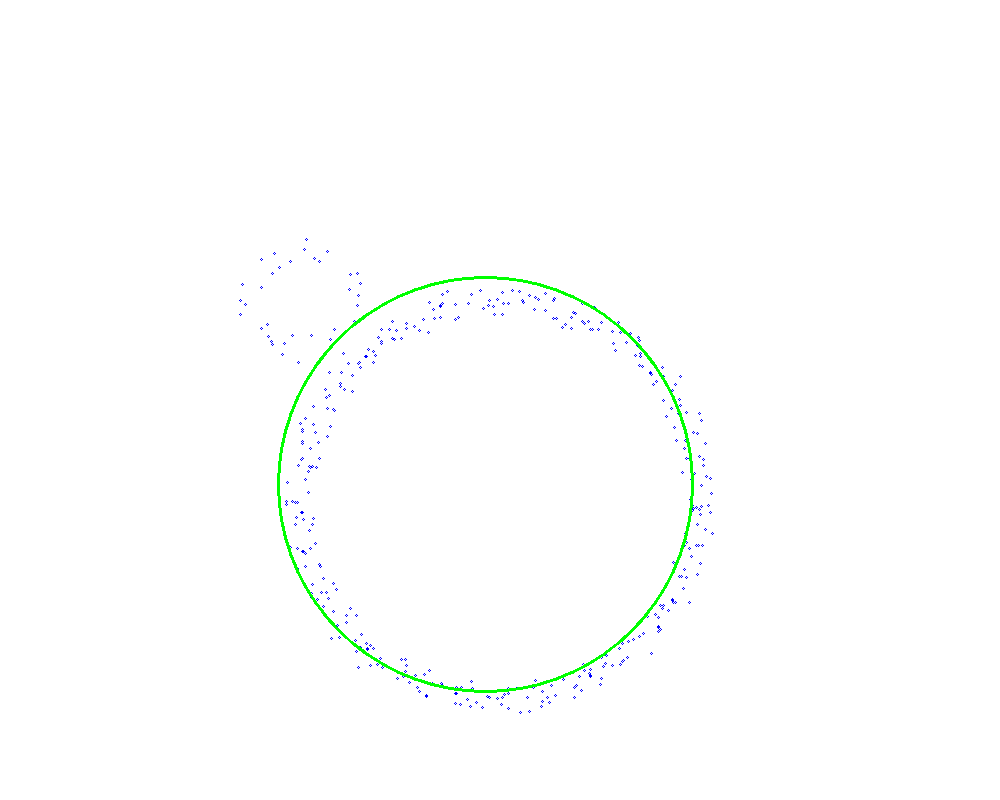 平均绝对误差拟合效果
平均绝对误差拟合效果
 两者对比
两者对比